Varianta 83
Prof: Grecu Maria
- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.
- Timpul efectiv de lucru: 2 ore.
SUBIECTUL I – Pe foaia de examen se trec doar rezultatele. ( 30 de puncte)
(5p) 1. Rezultatul calculului \(3\sqrt{5}+7\sqrt{5}-8\sqrt{5}\)este egal cu .....
(5p) 2. Media aritmetică a numerelor 2,75 şi 14,8 este .....
(5p) 3. Probabilitatea ca din 4500 de sticle de băutură răcoritoare să nimereşti una din cele 30 de sticle pe al cărei capac scrie „ Ai câştigat 100 RON’’ este de .....
(5p) 4. Linia mijlocie a unui trapez are lungimea de 16 cm, iar segmentul determinat de diagonale pe aceasta este de 10 cm. Lungimea bazei mari este de ..... cm.
(5p) 5. O prismă triunghiulară regulată are înălţimea de 10 cm. Dacă muchia bazei are lungimea de 6 cm, atunci volumul prismei este egal cu ..... cm3.
(5p) 6. La un post de televiziune s-au făcut măsurători pe parcursul intervalului orar 16-24 din ziua de 1 octombrie 2010, pentru a vedea cum fluctuează numărul telespectatorilor.Rezultatele au fost ilustrate prin graficul următor:
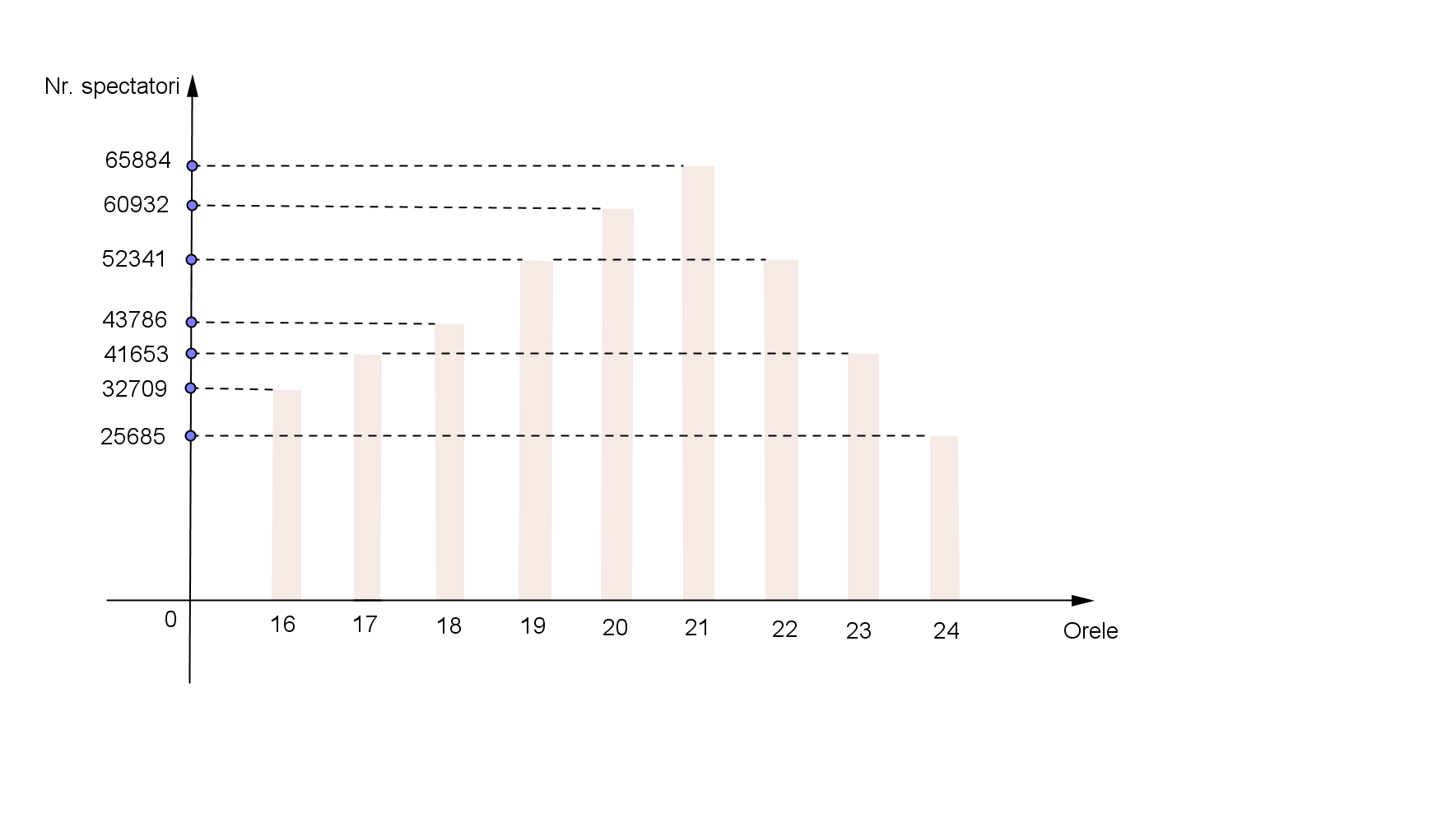
Numărul telespectatorilor care au vizionat postul de televiziune între 16-24 este .....
SUBIECTUL II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)
(5p) 1. Desenaţi cubul ABCDEFGH şi notaţi cu O centrul bazei.
(5p) 2. Să se arate că numărul \(2\cdot \left( 1+2+3+........+2010 \right)+2011\)este pătrat perfect.
(5p) 3. După ce a citit 60% din numărul paginilor unei cărţi şi apoi 20% din rest, unui elev i-au mai rămas de citit 48 de pagini pentru a termina cartea. Câte pagini a citit elevul?
4. Se consideră funcţia: \(f:\mathbb{R}\to \mathbb{R}\), \(f\left( x \right)=2x+3\).
(5p) a) Să se determine \(m\in \mathbb{N}\)astfel ca punctul A(3m+2,m2) să aparţină graficului funcţiei
(5p) b) Să se determine punctul de pe graficul funcţiei, a cărui abscisă este egală cu o treime din ordonată.
(5p) 5. Ştiind că \({{x}^{2}}+{{y}^{2}}-8x+12y+48=0\), să se determine căror intervale le aparţin x şi y.
SUBIECTUL III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)
- Pe un teren în formă de dreptunghi se construieşte o fântână arteziană cu bazinul în formă de cerc, ca în figura alăturată. Se ştie că AB=5m, BC=3m iar diametrul cercului este de 2m. Adâncimea bazinului este de 1,20m.
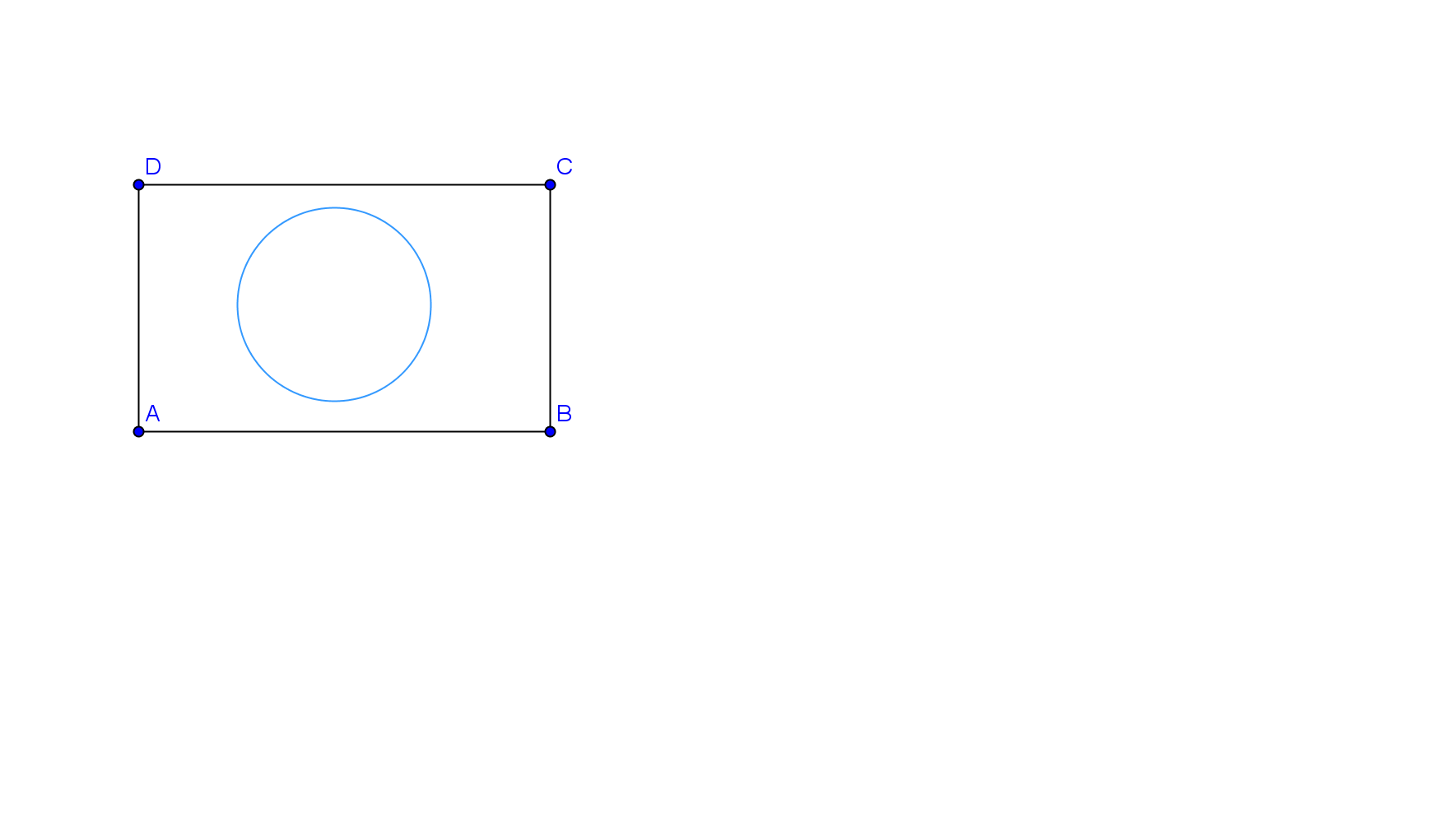
(5p) a) Să se calculeze câţi m2 de gazon trebuie cumpăraţi pentru a acoperi porţiumea de teren aflată în afara bazinului.( \(\pi =3,14\))
(5p) b) În cât timp se umple bazinul cu apă dacă debitul apei este de 1,5 l apă pe secundă? (\({{V}_{bazin}}=\pi {{R}^{2}}\cdot h\))
(5p) c) Ştiind că la fiecare 120 s apa care ţâşneşte işi schimbă culoarea, să se afle de câte ori îşi schimbă apa culoarea în intervalul în care se umple bazinul.
- În desenul următor este reprezentată o casă. Se ştie că AB=8m, BC=3,5m, CN=5m iar BE=4,5m.
(5p) a) Cât costă ţigla necesară pentru acoperişul casei ştiind că 1m2 de ţiglă costă 4 lei?
(5p) b) Pereţii exteriori sunt pulverizaţi cu o substanţă pentru a fi protejaţi împotriva umezelii.Dacă un flacon conţine 300 ml de substanţă, să se calculeze câte flacoane sunt necesare pentru a acoperi pereţii, ştiind că 20 ml de substanţă acoperă o suprafaţă de 4 m2.
(5p) c) În jurul casei se construieşte o alee asfaltată având lăţimea de 50 cm. Pe părţile laterale ale aleii se pun mici felinare, din 3 în 3 m. Câte felinare sunt necesare pentru a ilumina casa?


