Varianta 164

Prof: Iuliana Traşcă

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Rezultatul calculului   $\frac{13}{4}+\frac{3}{4}-2$ este...

(5p)     2. Valoarea lui x pentru care fracţia  $\frac{2x-14}{10}$ este echiunitară…

(5p)     3. Un triunghi dreptunghic isoscel cu o catetă $9\sqrt{2}\text{ cm}$ are ipotenuza de ...cm

(5p)     4. Descompunerea în factori a expresiei $81{{x}^{2}}-121{{y}^{2}}$ este...

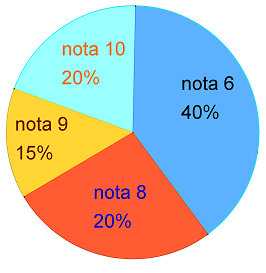
(5p)     5. La o teză de matematică s-au obţinut notele din diagrama de mai jos. În  clasă  sunt 30 de elevi, numărul elevilor care au luat nota zece este...

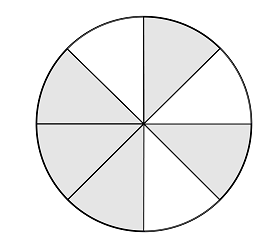
(5p)     6. Fracţia reprezentată de suprafaţa haşurată din figura alăturată este ...

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi, pe foaia de examen, cubul ABCDMNPQ şi diagonala AP

(5p)     2. Numerele x, y sunt direct proporţionale cu 8 şi 10, numerele y şi z sunt invers proporţionale cu 6 şi 5, iar x+y+z=30 Aflaţi numerele x, y şi z.

(5p)     3.  În dreptunghiul MNPQ fie S proiecţia punctului N pe diagonala[ MP]. Dacă NS= 15 cm, MS=45 cm, calculaţi aria dreptunghiului MNPQ.

4.  Fie $f:\mathbb{R}\to \mathbb{R}$, f(x)= 5x-2

(5p)    a)  Aflaţi a $\in \mathbb{R}$ ştiind că $A\left( \frac{3\left| a-2 \right|+7}{5};\frac{5\left| a-2 \right|+11}{2} \right)$aparţine graficul funcţiei f.

(5p)    b) Aflaţi $n\in {{\mathbb{R}}_{+}}$ pentru care ${{f}^{2}}\left( n \right)+8\cdot f\left( n+1 \right)-49=0$

(5p)     5. Aflaţi valoarile lui $x\in \mathbb{Z}$astfel încât $a=\frac{\left( {{11}^{62}}+\left| {{10}^{93}}-{{11}^{62}} \right| \right):{{10}^{92}}}{\left( {{19}^{34}}+\left| {{19}^{34}}-{{10}^{51}} \right| \right):{{10}^{50}}}+\frac{7}{x-2}\in \mathbb{Z}$

SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. Într-un trapez isoscel în care$BC\parallel AD$si AB=CD, $BD\bot DC$, BD=12 m, DC=5 m, $DM\bot BC,M\in [BC]$, $AN\bot BC,N\in [BC]$ , MC=1 m . În exteriorul acestui trapez se construieşte dreptunghiul ADEF, având lungimea egală cu baza mică a trapezului, iar lăţimea cu 8 m mai mică decât lungimea sa.

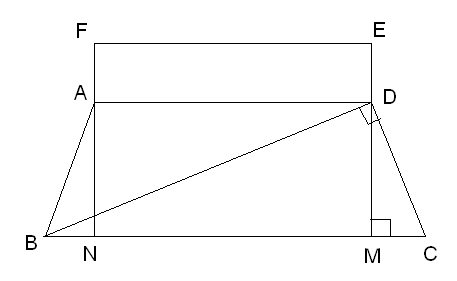
 (5p)  a) Aflaţi BN, BC,AD, AF;

 (5p)  b) Calculaţi${{A}_{ABCD}},{{A}_{ABD}}$;

 (5p)  c) Aflaţi${{A}_{ABDEF}}$. Suprafaţa ABDEF se însămânţează cu grâu. Grâul este ambalat în pungi. Cantitatea de grâu dintr-o pungă ajunge pentru a însămânţa  $\frac{33}{13}{{\text{m}}^{2}}$. Câte pungi sunt necesare pentru a însămânţa  întreaga suprafată ABDEF ?

1. Fie VABC o piramidă triunghiulară regulată cu O centrul bazei.     Dacă$VO\bot (ABC)$, AO=6 cm şi VO=8 cm , determinaţi:

(5p)  a) $VA,BM$şi ${{a}_{b}}$ (unde M este mijlocul lui $\left[ AC \right]$);

(5p)  b) $AB$,${{A}_{b}},{{A}_{l}}$;