Varianta 181

Prof: Constantin Corina - Carmen

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Rezultatul calculului $2015-2015:5$ este egal cu ...

(5p)     2. Opusul numărului 28 adunat cu răsturnatul numărului 28 este ..

(5p)     3. Dacă $A=\left[ -3,7 \right)$ şi $B=\left( -\infty ,0 \right)$, atunci mulţimea $A\cap B$este egală cu ...

(5p)     4. Un dreptunghi este echivalent cu un pătrat. Dacă latura pătratului este de 4 cm, atunci aria dreptunghiului este egală cu ... cm².

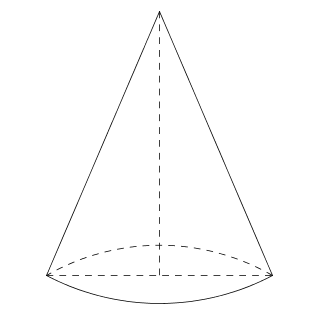
(5p)     5. În Figura 1 este reprezentat un con circular drept cu raza de 3 cm şi înălţimea de 4 cm. Aria conului este egală cu ... $\pi$ cm².

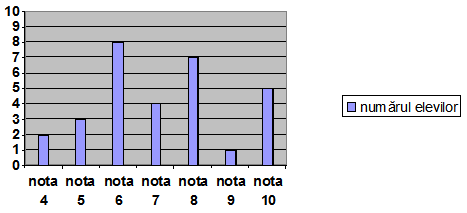
(5p)     6. În graficul de mai jos sunt prezentate rezultatele elevilor unei clase la testul de matematică. Numărul elevilor care au cel mult nota 6 este egal cu ...

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi, pe foaia de examen, o prismă triunghiulară regulată ABCDEF.

(5p)     2. Numerele x şi y sunt direct proporţionale cu numerele 4 şi 6. Determinaţi numerele x şi y, dacă $2x+3y=52$.

(5p)     3. Numărul elevilor unei şcoli este cuprins între 600 şi 700. Dacă îi grupăm câte 6, câte 9 sau câte 15, rămân de fiecare dată 4 elevi. Determinaţi câţi elevi are şcoala.

 4. Se consideră funcţia $f:\mathbb{R}\to \mathbb{R}$,$f\left( x \right)=-3x+a$, unde a este un număr real.

(5p)    a) Determinaţi numărul real a dacă $\left| f\left( -8 \right) \right|\le 2$.

(5p)    b) Aflaţi distanţa de la O la graficul funcţiei f, unde O este originea sistemului de coordonate xOy, dacă $a=-1$.

(5p)     5. Se consideră expresia $E\left( x \right)=\frac{{{x}^{2}}+x-20}{{{x}^{2}}-2x+1}:\frac{{{\left( x-1 \right)}^{2}}-9}{{{x}^{2}}+x-2}$, unde $x\in \mathbb{R}-\left\{ -2,1,4 \right\}$. Determinaţi numărul real a, $a\notin \left\{ -2,1,4 \right\}$, ştiind că $E\left( a \right)=3$.

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. O grădină sub formă de disc este prevăzută cu o piscină sub formă de romb, ca în Figura 2. Raza discului este de 6 m, iar măsura unui unghi al rombului este de 60⁰. Piscina este înconjurată de gazon.

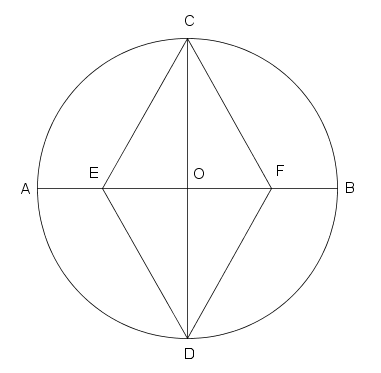
 (5p)  a) Arătaţi că latura rombului este egală cu $4\sqrt{3}$m.

 (5p)  b) Determinaţi suprafaţa gazonului, dacă $\pi \simeq 3,14$ şi $\sqrt{3}\simeq 1,73$.

 (5p)  c) Un înotător porneşte din punctul E şi străbate piscina pe distanţa cea mai mică pentru a ajunge la latura opusă. Determinaţi această distanţă.

2. Un depozit de mingi are formă de paralelipiped dreptunghic, iar o minge formă de sferă, ca în Figura 3. Dimensiunile depozitului sunt: $L=8$m, $l=6$m şi $h=5$m, iar raza unei mingi este 15 cm.

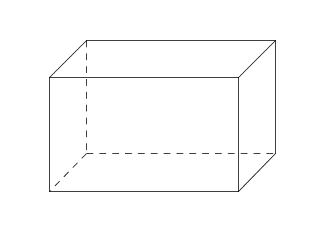
(5p)  a) Aflaţi aria şi volumul unei mingi.

(5p)  b) Câte mingi încap în depozit?

(5p)  c) Dacă o minge costă 25 lei, câţi lei costă toate mingile din depozit?